About the Measure tool and its limitations¶

The Sonic Visualiser Help reference describes the Measure tool like this:

The measure tool enables you to obtain measurements in scale units (such as time in the X coordinate, or whatever the Y coordinate of the current layer represents) corresponding to certain pixel positions. To measure a region, just click and drag a rectangle covering it, using the left mouse button with the measure tool selected ...
It's important to note that the measurements shown in this way are based entirely on the pixel coordinates of the measurement rectangle, not on properties of the data being displayed.

The measure tool also has the ability to produce an automatic bounding box for a graphical feature, when double-clicked:

The area enclosed by the rectangle is based on the extent of similarly-coloured pixels surrounding the click position: it is entirely graphical, involving no audio analysis, and so depends on the gain and colour scheme in use in the spectrogram.

Here's an example of what that means in terms of the practical limitations of the tool.

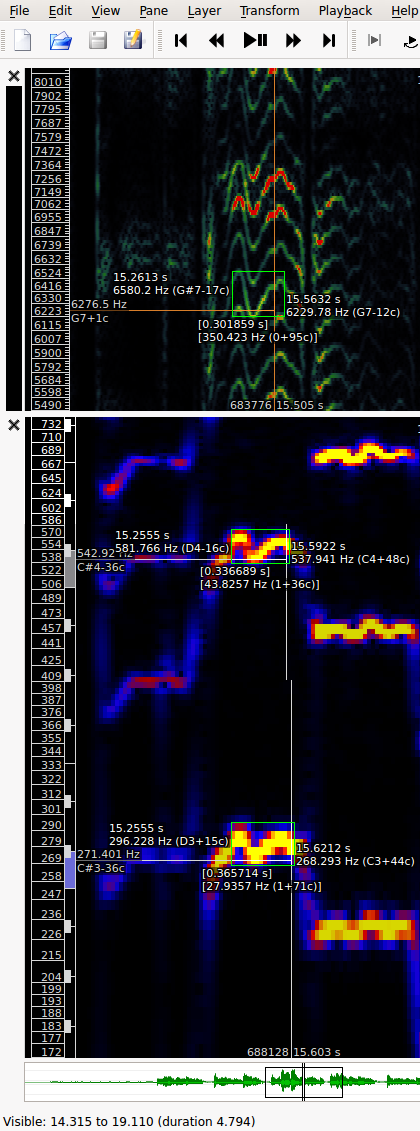
This is a recording of a singer, with vibrato. For this illustration I have switched off all of the spectrogram interpolation options in the preferences. The image shown here is a composite of three separately-highlighted measure boxes, because it isn't actually possible to highlight all three at once in SV. Let's imagine we want to measure the variation in pitch of the singer's vibrato about a nominal note pitch.

The bottom measurement box shows a box with a frequency-scale range from 268.3 to 296.2Hz. These are the values that you would find if you took the green-line pixel positions and read them off against the scale on the left, interpolating appropriately (and taking into account that it's a log frequency scale). The frequency difference from top to bottom is 27.9Hz, but we want it in semitones, which corresponds to a frequency ratio rather than a frequency difference. Our ratio here is 296.2/268.3 = 1.104, for a semitone range of 12 * log2(1.104) = 1.712 semitones.

How accurate is that as an estimate of the singer's vibrato range? This is an 8192-bin spectrogram; the bin resolution of 44100/8192 = 5.38Hz corresponds to 0.34 semitones at this pitch -- that is, 12 * log2((268.3 + 5.38) / 268.3). Not very accurate.

Moving up, the middle measurement box shows the same rectangle around a higher harmonic of the same note. This time the range from 537.9 to 581.8Hz gives a 1.36 semitone range. This harmonic has double the frequency of the first; if we just doubled the frequency limits from the first box, we'd have 536.6 to 592.4Hz so this is tighter at both top and bottom, but particularly at the top where our placement of the green line was a bit optimistic in the first box.