SyntheticTest » History » Version 12
« Previous -
Version 12/13
(diff) -
Next » -
Current version
Chris Cannam, 2013-11-18 05:11 PM
Synthetic test material¶
Sinusoid at fs/4¶
In Yeti terms:
testStream = manipulate.withDuration 64 (syn.sinusoid 8 2);
cq = cqt { maxFreq = testStream.sampleRate/2, minFreq = 1, binsPerOctave = 4 } testStream;
Or to put it another way (in MATLAB this time):
test = [0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1,0,1,0,-1 ]; out = cqt(test,1,4,4,8)
That is, a 64-sample input of 8Hz sample rate containing a sinusoid at fs/4, transformed using CQ parameters fmin = 1, fmax = 4 (or fs/2), and bpo = 4.
Data from MATLAB implementation¶
actual fmin = 1.1892 octaves = 2 weight = 16.3452 drop = 3 kernel size = 32x20 output size = 8x59
and the output (magnitudes only):
Columns 1 through 8
0.0001 0 0.0002 0 0.0001 0 0.0002 0
0.0001 0 0.0001 0 0.0002 0 0.0004 0
0.0001 0 0.0001 0 0.0003 0 0.0011 0
0.0002 0 0.0000 0 0.0003 0 0.0013 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
Columns 9 through 16
0.0011 0 0.0044 0 0.0980 0 0.3084 0
0.0018 0 0.0082 0 0.0468 0 0.3858 0
0.0050 0 0.0243 0 0.1211 0 0.6447 0
0.0065 0 0.0309 0 0.1543 0 0.8114 0
0 0 0 0 0.0002 0.0086 0.2742 1.1185
0 0 0 0 0.0011 0.0010 0.0711 0.7025
0 0 0 0 0.0001 0.0002 0.0099 0.5388
0 0 0 0 0.0001 0.0019 0.0006 0.4688
Columns 17 through 24
0.3962 0 0.2374 0 0.0484 0 0.0032 0
0.6804 0 0.3858 0 0.0468 0 0.0082 0
1.1968 0 0.6447 0 0.1211 0 0.0243 0
1.6297 0 0.8114 0 0.1544 0 0.0309 0
2.1085 2.4893 2.4383 2.4312 2.4314 2.4307 2.4311 2.4311
1.3506 0.9697 0.7693 0.7692 0.7688 0.7693 0.7691 0.7691
0.8193 0.0813 0.0491 0.0649 0.0499 0.0643 0.0493 0.0646
0.7188 0.0108 0.0492 0.0010 0.0493 0.0001 0.0488 0.0000
Columns 25 through 32
0.0007 0 0.0003 0 0.0006 0 0.0019 0
0.0019 0 0.0005 0 0.0004 0 0.0032 0
0.0051 0 0.0012 0 0.0019 0 0.0086 0
0.0062 0 0.0008 0 0.0021 0 0.0111 0
2.4311 2.4311 2.4311 2.4311 2.4311 2.4311 2.4311 2.4311
0.7691 0.7691 0.7691 0.7691 0.7691 0.7691 0.7691 0.7691
0.0493 0.0646 0.0493 0.0646 0.0493 0.0646 0.0493 0.0646
0.0488 0.0000 0.0488 0.0000 0.0488 0.0000 0.0488 0.0000
Columns 33 through 40
0.0168 0 0.1633 0 0.3646 0 0.3646 0
0.0143 0 0.1184 0 0.5325 0 0.6406 0
0.0414 0 0.2181 0 0.9118 0 1.1190 0
0.0532 0 0.2679 0 1.1926 0 1.5069 0
2.4311 2.4309 2.4305 2.4835 2.3188 1.4767 0.4927 0.0454
0.7692 0.7695 0.7692 0.7707 1.1679 1.2359 0.4175 0.0087
0.0494 0.0639 0.0494 0.0651 0.3139 0.8970 0.2914 0.0008
0.0490 0.0000 0.0490 0.0024 0.2044 0.8567 0.1557 0.0024
Columns 41 through 48
0.1633 0 0.0168 0 0.0019 0 0.0003 0
0.2373 0 0.0229 0 0.0052 0 0.0012 0
0.3956 0 0.0706 0 0.0144 0 0.0029 0
0.4838 0 0.0905 0 0.0184 0 0.0037 0
0.0000 0.0002 0 0 0 0 0 0
0.0012 0.0004 0 0 0 0 0 0
0.0002 0.0007 0 0 0 0 0 0
0.0002 0.0000 0 0 0 0 0 0
Columns 49 through 56
0.0003 0 0.0000 0 0.0000 0 0.0000 0
0.0003 0 0.0000 0 0.0000 0 0.0000 0
0.0006 0 0.0001 0 0.0000 0 0.0000 0
0.0009 0 0.0002 0 0.0000 0 0.0000 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
Columns 57 through 59
0.0000 0 0.0000
0.0000 0 0.0000
0.0000 0 0.0000
0.0000 0 0.0000
0 0 0
0 0 0
0 0 0
0 0 0
Data from Yeti implementation¶
Process data¶
sampleRate = 8
maxFreq = 4
minFreq = 1
actualMinFreq = 1.189207115002721
octaves = 2
binsPerOctave = 4
overall output size = {columns=40, rows=8}
Kernel data¶
That is,
> (load cqtkernel).makeKernel { binsPerOctave = 4, maxFreq = 4, sampleRate = 8 }
gives
minFreq = 2.378414230005442, bigQ = 5.285213507883246, maxNK = 18, minNK = 11, atomHop = 3, firstCentre = 9, fftSize = 32
winNr = 5, lastCentre = 21, fftHop = 15
density = 0.6953125 (445 of 640)
weight = 16.34515230237943
{
atomSpacing = 3,
atomsPerFrame = 5,
bigQ = 5.285213507883246,
binsPerOctave = 4,
fftHop = 15,
fftSize = 32,
firstCentre = 9,
kernel = { ... , size = { columns = 32, rows = 20 } },
maxFreq = 4,
minFreq = 2.378414230005442
}
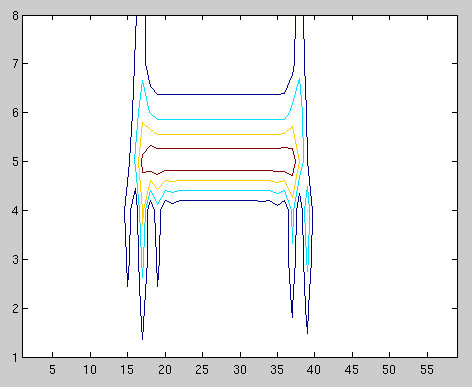
Output¶
Notes on this:
- We should expect the top octave (which is the bottom half of the matrix, in this printout and the MATLAB one above) to be identical in both versions. It isn't quite.
- The bottom octave can be expected to vary because the two implementations have different decimators.
- Alignment is clearly not done correctly, but we expect different alignment requirements for each octave anyway
- The repeating patterns in the Yeti output, in the top octave from roughly column 7 (counting from 1) to column 22 are comparable with those in the MATLAB from column 19 to column 36
- I can't see any such obvious alignment in the other octave
Columns 1 to 8 0.0062 0 0.1939 0 0.5393 0 0.6454 0 2.0E-4 0 0.0579 0 0.5993 0 1.0286 0 1.0E-4 0 0.0075 0 0.6026 0 1.757 0 6.0E-4 0 1.0E-4 0 0.4464 0 2.2625 0 8.0E-4 0.1289 0.7799 1.8196 2.4423 2.4596 2.4313 2.4312 4.0E-4 0.0086 0.4173 1.2368 1.1677 0.7713 0.7694 0.7692 0 3.0E-4 0.2913 0.8965 0.314 0.0646 0.0491 0.0646 0 0.0023 0.1558 0.8546 0.2042 3.0E-4 0.0487 0 Columns 9 to 16 0.357 0 0.0622 0 0.005 0 0.0036 0 0.5072 0 0.0268 0 0.035 0 0.0297 0 1.4134 0 0.7419 0 0.4654 0 0.2754 0 2.2998 0 1.3286 0 0.8006 0 0.422 0 2.4311 2.4304 2.4311 2.4311 2.4311 2.4311 2.4311 2.4311 0.7688 0.7692 0.7691 0.7691 0.7691 0.7691 0.7691 0.7691 0.0494 0.0646 0.0493 0.0645 0.0493 0.0645 0.0493 0.0645 0.0492 0 0.0487 0 0.0487 0 0.0487 0 Columns 17 to 24 0.0028 0 0.0032 0 0.0042 0 0.0356 0 0.0276 0 0.0281 0 0.0311 0 0.0364 0 0.1564 0 0.1849 0 0.3315 0 0.5455 0 0.1018 0 0.2055 0 0.5387 0 0.9529 0 2.4311 2.4311 2.4311 2.4311 2.4311 2.4311 2.459 2.442 0.7691 0.7691 0.7691 0.7691 0.7691 0.7694 0.7691 0.969 0.0493 0.0645 0.0493 0.0645 0.0497 0.0642 0.0492 0.0816 0.0487 0 0.0487 0 0.049 9.0E-4 0.0494 0.0087 Columns 25 to 32 0.2089 0 0.3834 0 0.3231 0 0.1176 0 0.1912 0 0.6183 0 0.5288 0 0.1079 0 0.9105 0 1.3187 0 0.6723 0 0.0493 0 1.572 0 1.856 0 0.6379 0 0.0053 0 1.8192 0.7802 0.1289 8.0E-4 3.0E-4 3.0E-4 0 0 1.3506 0.7023 0.0712 0.001 1.0E-4 2.0E-4 0 0 0.819 0.5381 0.0101 6.0E-4 2.0E-4 7.0E-4 0 0 0.7186 0.4668 4.0E-4 0.002 1.0E-4 0 0 0 Columns 33 to 40 0.0037 0 3.0E-4 0 4.0E-4 0 4.0E-4 0 5.0E-4 0 2.0E-4 0 1.0E-4 0 2.0E-4 0 0 0 1.0E-4 0 0 0 1.0E-4 0 0 0 2.0E-4 0 0 0 2.0E-4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0